Primo e secondo criterio di congruenza dei triangoli¶
Ricordiamo che due figure piane sono congruenti se sono sovrapponibili, cioè se è possibile spostare una sull’altra, senza deformarle, in modo che coincidano perfettamente.
In particolare, due triangoli sono sovrapponibili se hanno “ordinatamente” congruenti i tre lati ed i tre angoli. Con il termine ordinatamente intendiamo che, a partire da una coppia di vertici e procedendo lungo il contorno in senso orario oppure antiorario, incontriamo lati congruenti e vertici di angoli congruenti. Nel caso dei triangoli, questo succede esattamente quando angoli congruenti nei due triangoli sono compresi tra coppie di lati congruenti o, in maniera equivalente, quando sono opposti a lati congruenti.
I criteri di congruenza dei triangoli ci dicono che basta conoscere la congruenza di solo alcuni elementi dei due triangoli, generalmente tre elementi di un triangolo congruenti a tre elementi dell’altro triangolo, per poter affermare la congruenza di due triangoli, e quindi dedurne la congruenza degli altri elementi.
Un modo tradizionale di presentare l’argomento, dovuto allo stesso Euclide, è quello di “dimostrare” i primi due criteri di congruenza dei triangoli facendo uso della definizione di congruenza come “uguaglianza per sovrapposizione”, e di utilizzarli successivamente per la verifica di altre proprietà.
Secondo il matematico tedesco D. Hilbert (1862-1943), il primo criterio di congruenza è un assioma, il secondo criterio può essere dimostrato per assurdo attraverso il primo.
Presenteremo questi argomenti basilari alla maniera di Euclide.
Primo criterio di congruenza dei triangoli¶
Due triangoli sono congruenti se hanno congruenti due lati e l’angolo tra essi compreso.
Ipotesi:
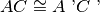
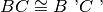
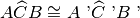
breakTesi:
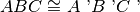
Dimostrazione. Vogliamo provare che il triangolo
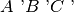 può essere portato a sovrapporsi perfettamente al triangolo
può essere portato a sovrapporsi perfettamente al triangolo
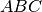 .
.
A tal proposito, portiamo il punto
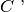 sul punto
sul punto
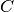 in modo tale che la semiretta
in modo tale che la semiretta
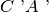 sia sovrapposta alla semiretta
sia sovrapposta alla semiretta
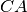 ed i punti
ed i punti
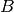 e
e
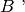 siano nello stesso semipiano individuato dalla retta
siano nello stesso semipiano individuato dalla retta
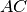 .
.
Dopo questo movimento, i triangoli potrebbero trovarsi nella posizione della figura a lato?
Vediamo perché questa situazione non è possibile. Abbiamo supposto per ipotesi
che i segmenti
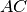 e
e
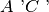 siano congruenti, pertanto se
siano congruenti, pertanto se
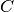 coincide con
coincide con
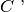 anche
anche
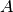 deve coincidere necessariamente con
deve coincidere necessariamente con
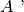 , mentre nella figura
, mentre nella figura
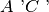 è maggiore di
è maggiore di
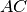 .
.
Allora i triangoli potrebbero trovarsi almeno nella seguente posizione, nella quale A e A’ coincidono?
Tuttavia nemmeno questa posizione è possibile poiché abbiamo supposto per
ipotesi che gli angoli
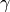 e
e
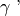 siano congruenti, mentre dalla figura risulta che
siano congruenti, mentre dalla figura risulta che
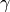 è maggiore di
è maggiore di
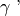 . Di conseguenza la semiretta per
. Di conseguenza la semiretta per
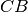 e la semiretta per
e la semiretta per
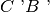 devono sovrapporsi, in quanto devono formare lo stesso angolo con la semiretta
per
devono sovrapporsi, in quanto devono formare lo stesso angolo con la semiretta
per
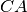 .
.
A questo punto, rimane da fissare la posizione di
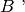 rispetto a
rispetto a
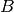 , cioè rimane da decidere se
, cioè rimane da decidere se
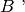 cade internamente al segmento
cade internamente al segmento
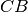 , come nella figura che segue, se
, come nella figura che segue, se
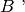 cade esternamente al segmento
cade esternamente al segmento
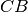 o se
o se
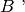 e
e
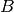 coincidono.
coincidono.
Poiché per ipotesi
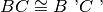 , il punto
, il punto
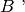 deve necessariamente coincidere con
deve necessariamente coincidere con
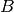 . Pertanto i vertici del triangolo
. Pertanto i vertici del triangolo
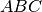 si sovrappongono ai vertici del triangolo
si sovrappongono ai vertici del triangolo
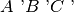 e di conseguenza i triangoli
e di conseguenza i triangoli
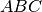 e
e
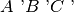 sono congruenti.Q.e.d.
sono congruenti.Q.e.d.
Primo criterio di congruenza dei triangoli¶
Due triangoli sono congruenti se hanno congruenti due angoli e il lato tra essi compreso.
Ipotesi:
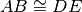 ,
,
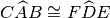 ,
,
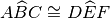 .
.
Tesi:
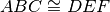 .
.
Dimostrazione. Vogliamo provare che il triangolo
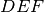 può essere portato a sovrapporsi perfettamente al triangolo
può essere portato a sovrapporsi perfettamente al triangolo
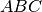 .
.
A tal proposito, in virtù della congruenza dei lati AB e DE, portiamo a sovrapporre il segmento DE al segmento AB in maniera tale che D coincida con A, E coincida con B, e i punti C ed F siano nello stesso semipiano individuato dalla retta AB.
I due triangoli potrebbero trovarsi nella seguente posizione?
Dalla congruenza degli angoli
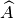 e
e
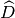 , segue che la semiretta DF sarà sovrapposta alla semiretta AC; analogamente,
dalla congruenza degli angoli
, segue che la semiretta DF sarà sovrapposta alla semiretta AC; analogamente,
dalla congruenza degli angoli
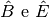 , segue che la semiretta EF sarà sovrapposta alla semiretta BC. Dunque C ed F
devono necessariamente coincidere, perché sono l’unica intersezione di due
rette incidenti. Poiché i tre vertici si sono sovrapposti, i due triangoli sono
completamente sovrapposti e quindi sono congruenti. Q.e.d.
, segue che la semiretta EF sarà sovrapposta alla semiretta BC. Dunque C ed F
devono necessariamente coincidere, perché sono l’unica intersezione di due
rette incidenti. Poiché i tre vertici si sono sovrapposti, i due triangoli sono
completamente sovrapposti e quindi sono congruenti. Q.e.d.
Esempio
Si considerino due rette incidenti,
 ed
ed
 , ed il loro punto in comune
, ed il loro punto in comune
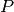 . Sulle semirette opposte di origine
. Sulle semirette opposte di origine
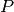 si prendano punti equidistanti da
si prendano punti equidistanti da
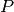 , come in figura, in maniera tale che
, come in figura, in maniera tale che
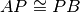 ,
,
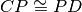 . Dimostra che, unendo i quattro punti in modo da costruire un quadrilatero, i
quattro triangoli che si vengono a formare sono a due a due congruenti:
. Dimostra che, unendo i quattro punti in modo da costruire un quadrilatero, i
quattro triangoli che si vengono a formare sono a due a due congruenti:
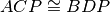 ,
,
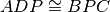 .
.
Realizziamo il disegno ed esplicitiamo ipotesi e tesi
Ipotesi
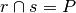
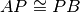
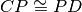
Tesi
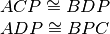
Dimostrazione. I triangoli
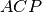 e
e
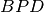 hanno:
hanno:
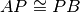 per ipotesi,
per ipotesi,
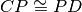 per ipotesi,
per ipotesi,
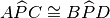 perché opposti al vertice. Pertanto sono congruenti per il 1° criterio di
congruenza dei triangoli.
perché opposti al vertice. Pertanto sono congruenti per il 1° criterio di
congruenza dei triangoli.
Analogamente, i triangoli
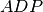 e
e
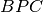 hanno: … … … … … … … …
hanno: … … … … … … … …
Esempio
- Si considerino un segmento AB ed il suo punto medio M. Si tracci una generica retta r passante per M e distinta dalla retta per AB. Si traccino inoltre due semirette di origine rispettivamente A e B, situate nei due semipiani opposti rispetto alla retta per AB, che intersechino la retta r rispettivamente in C e in D e che formino con la retta per AB due angoli congruenti (vedi figura). Detti C e D i rispettivi punti d’intersezione delle due semirette con la retta r, dimostra che i triangoli AMC e BMD sono congruenti.
Ipotesi:
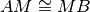
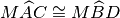
Tesi:
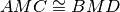
Dimostrazione. I segmenti
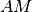 e
e
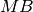 sono congruenti in quanto
sono congruenti in quanto
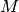 è il punto medio di
è il punto medio di
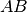 , gli angoli di vertice
, gli angoli di vertice
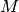 sono congruenti perché opposti al vertice, gli angoli di vertice
sono congruenti perché opposti al vertice, gli angoli di vertice
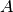 e
e
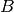 sono congruenti per costruzione. Allora i triangoli
sono congruenti per costruzione. Allora i triangoli
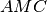 e
e
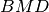 sono congruenti per il secondo criterio di congruenza dei triangoli.
sono congruenti per il secondo criterio di congruenza dei triangoli.
Esercizi sul 1° e 2° criterio di congruenza dei triangoli
Esercizi¶
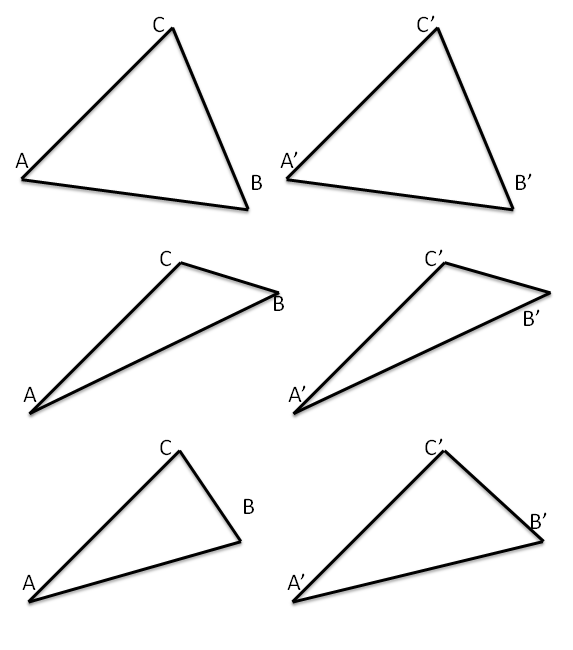
Per ciascuna delle seguenti coppie di triangoli indica se sono congruenti ed eventualmente per quale criterio.
- Si sa che sono congruenti i lati
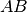 con
con
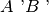 e
e
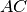 con
con
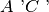 , l’angolo in
, l’angolo in
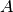 con l’angolo
con l’angolo
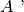 . I triangoli sono congruenti? Se sì, per
. I triangoli sono congruenti? Se sì, per - Si sa che sono congruenti i lati
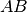 con
con
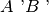 e gli angoli in
e gli angoli in
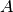 con
con
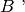 e
e
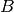 con
con
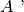 . I triangoli sono congruenti? Se sì, per
. I triangoli sono congruenti? Se sì, per - Si sa che sono congruenti ilati
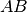 con
con
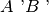 e
e
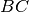 con
con
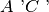 , l’angolo in
, l’angolo in
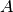 con
con
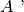 . I due triangoli sono congruenti? Se sì, per
. I due triangoli sono congruenti? Se sì, per
- Si sa che sono congruenti i lati
In un triangolo
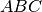 prolunga la mediana
prolunga la mediana
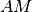 di un segmento
di un segmento
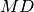 congruente a
congruente a
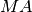 . Dimostra che il triangolo
. Dimostra che il triangolo
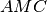 è congruente al triangolo
è congruente al triangolo
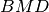 e che il triangolo
e che il triangolo
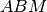 è congruente al triangolo
è congruente al triangolo
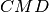 .
.Due triangoli
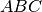 e
e
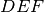 hanno il lati
hanno il lati
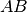 e
e
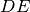 congruenti, hanno inoltre gli angoli esterni ai vertici
congruenti, hanno inoltre gli angoli esterni ai vertici
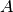 e
e
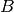 rispettivamente congruenti agli angoli esterni ai vertici
rispettivamente congruenti agli angoli esterni ai vertici
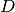 e
e
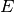 . Dimostra che i due triangoli sono congruenti.
. Dimostra che i due triangoli sono congruenti.Si consideri il segmento
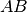 e per il suo punto medio
e per il suo punto medio
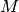 si tracci una retta r qualsiasi. Su tale semiretta, da parti opposte rispetto
a
si tracci una retta r qualsiasi. Su tale semiretta, da parti opposte rispetto
a
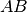 , si prendano due punti
, si prendano due punti
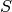 e
e
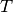 tali che
tali che
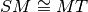 . Dimostrare che i triangoli
. Dimostrare che i triangoli
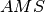 e
e
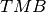 sono congruenti.
sono congruenti.Due triangoli rettangoli sono congruenti se hanno rispettivamente congruenti i due cateti.
Due triangoli rettangoli sono congruenti se hanno congruenti un cateto e l’angolo acuto adiacente ad esso.
Due triangoli isosceli sono congruenti se hanno congruenti l’angolo al vertice e i due lati obliqui.
Nel triangolo isoscele
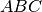 , di base
, di base
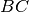 , prolunga la bisettrice
, prolunga la bisettrice
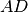 di un segmento
di un segmento
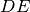 . Dimostra che
. Dimostra che
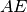 è bisettrice dell’angolo
è bisettrice dell’angolo
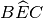 .. Warning, unrecognized:
{urn:oasis:names:tc:opendocument:xmlns:text:1.0}bookmark
.. Warning, unrecognized:
{urn:oasis:names:tc:opendocument:xmlns:text:1.0}bookmarkDati due triangoli congruenti
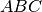 e
e
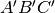 , si considerino sui lati
, si considerino sui lati
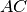 e
e
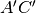 due punti
due punti
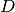 e
e
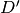 tali che
tali che
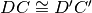 . Dimostrare che
. Dimostrare che
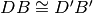 .
.Siano ABC e DEF due triangolo congruenti. Sui lati congruenti AB e DE prendi il punto G su AB e H su DE, in modo che
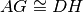 . Dimostra che anche GC è congruente ad HF.
. Dimostra che anche GC è congruente ad HF.In un triangolo ABC, sul prolungamento del lato AB, dalla parte di B, prendi un punto D tale che
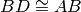 , analogamente sul prolungamento del lato CB, dalla parte di B, prendi un
punto E tale che
, analogamente sul prolungamento del lato CB, dalla parte di B, prendi un
punto E tale che
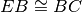 . Dimostra che la mediana
. Dimostra che la mediana
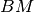 del triangolo
del triangolo
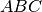 è allineata con la mediana
è allineata con la mediana
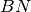 del triangolo
del triangolo
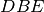 , ossia che l’angolo formato dalle due mediane è un angolo piatto.
, ossia che l’angolo formato dalle due mediane è un angolo piatto.Del triangolo
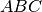 prolunga il lato
prolunga il lato
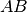 di un segmento
di un segmento
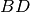 congruente a
congruente a
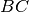 , analogamente prolunga il lato
, analogamente prolunga il lato
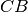 di un segmento
di un segmento
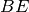 congruente ad
congruente ad
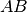 . Traccia la bisettrice
. Traccia la bisettrice
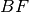 del triangolo
del triangolo
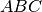 e la bisettrice
e la bisettrice
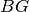 del triangolo
del triangolo
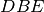 . Dimostra che
. Dimostra che
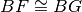 .
.Nel triangolo
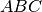 traccia la bisettrice
traccia la bisettrice
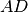 dell’angolo in
dell’angolo in
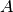 . Con origine in
. Con origine in
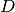 traccia due semirette che incontrano rispettivamente
traccia due semirette che incontrano rispettivamente
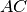 in
in
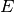 e
e
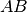 in
in
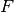 , in modo che
, in modo che
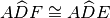 . Dimostra che il triangolo
. Dimostra che il triangolo
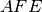 è un triangolo isoscele.
è un triangolo isoscele.Nel triangolo
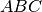 con
con
 traccia la bisettrice
traccia la bisettrice
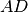 dell’angolo in
dell’angolo in
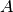 . Per il punto
. Per il punto
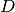 traccia la perpendicolare alla bisettrice
traccia la perpendicolare alla bisettrice
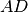 . Detti
. Detti
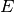 ed
ed
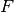 i punti in cui la perpendicolare incontra rispettivamente i lati
i punti in cui la perpendicolare incontra rispettivamente i lati
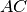 e
e
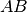 , dimostra che
, dimostra che
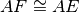 .
.Sui prolungamenti oltre
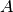 del lato
del lato
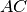 , oltre
, oltre
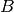 del lato
del lato
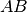 e oltre
e oltre
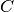 del lato
del lato
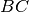 di un triangolo equilatero
di un triangolo equilatero
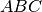 si considerino i segmenti congruenti
si considerino i segmenti congruenti
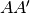 ,
,
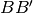 ,
,
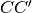 . Dimostrare che il triangolo
. Dimostrare che il triangolo
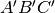 è ancora equilatero.
è ancora equilatero.Dato l’angolo convesso
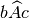 si considerino su
si considerino su
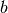 i due punti
i due punti
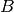 e
e
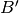 , su c si considerino i punti
, su c si considerino i punti
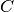 e
e
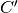 , tali che
, tali che
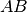 e
e
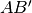 siano rispettivamente congruenti con
siano rispettivamente congruenti con
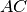 e con
e con
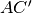 . Dimostrare che
. Dimostrare che
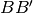 e
e
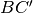 sono rispettivamente congruenti con
sono rispettivamente congruenti con
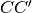 e
e
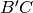 .
.Dato un segmento
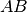 , condurre per il suo punto medio
, condurre per il suo punto medio
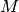 una qualsiasi retta r e considerare su di essa, da parti opposte rispetto ad
una qualsiasi retta r e considerare su di essa, da parti opposte rispetto ad
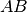 , due segmenti congruenti
, due segmenti congruenti
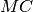 e
e
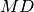 . Dimostrare che i triangoli
. Dimostrare che i triangoli
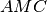 e
e
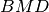 sono congruenti.
sono congruenti.Sui lati dell’angolo
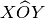 si considerino i punto
si considerino i punto
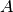 e
e
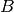 tali che
tali che
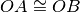 . Sia
. Sia
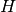 un punto della bisettrice dell’angolo tale che
un punto della bisettrice dell’angolo tale che
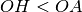 . Siano
. Siano
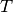 il punto di intersezione di
il punto di intersezione di
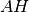 con
con
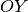 e
e
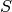 il punto di intersezione di
il punto di intersezione di
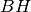 con
con
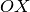 . Dimostrare che
. Dimostrare che
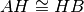 e
e
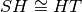 .
.Si consideri un punto
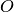 interno al triangolo
interno al triangolo
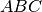 e si congiunga tale punto con i vertici
e si congiunga tale punto con i vertici
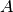 e
e
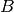 del triangolo. Si prolunghino i segmenti
del triangolo. Si prolunghino i segmenti
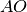 e
e
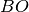 oltre
oltre
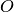 di due segmenti
di due segmenti
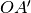 e OB’ rispettivamente congruenti ai suddetti segmenti. Dimostrare che i
segmenti AB e A’B’ sono congruenti.
e OB’ rispettivamente congruenti ai suddetti segmenti. Dimostrare che i
segmenti AB e A’B’ sono congruenti.Si considerino i triangoli congruenti ABC e A’B’C’ e si prolunghino i lati AB e A’B’ di due segmenti
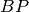 e
e
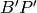 tra loro congruenti. Si prolunghino inoltre i lati
tra loro congruenti. Si prolunghino inoltre i lati
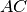 e
e
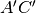 di due segmenti
di due segmenti
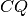 e
e
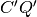 tra loro congruenti. Si dimostri che sono congruenti i triangoli
tra loro congruenti. Si dimostri che sono congruenti i triangoli
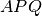 e
e
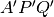 ;
;
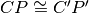 ,
,
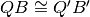 .
.Sui lati a e b di un angolo di vertice
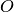 prendi i punti
prendi i punti
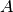 e
e
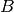 sulla semiretta a e i punti
sulla semiretta a e i punti
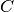 e
e
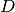 sulla semiretta b, in modo che
sulla semiretta b, in modo che
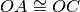 e
e
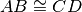 . Sia
. Sia
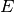 il punto di intersezione di
il punto di intersezione di
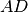 con
con
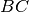 . Dimostra che sono congruenti i triangoli
. Dimostra che sono congruenti i triangoli
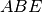 e
e
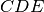 .
.Sui lati di un angolo convesso
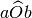 si prendano i due punti
si prendano i due punti
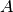 e
e
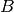 tali che
tali che
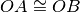 . Sia
. Sia
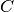 un punto della bisettrice. Dimostra che i triangoli
un punto della bisettrice. Dimostra che i triangoli
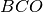 e
e
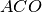 sono congruenti.
sono congruenti.